Adapting the Lattice-Boltzmann Model for Efficient Airflow Modeling inside the View Frustum

 

Independent Study Project by Leonid Velikovich

Advisor: Amitabh Varshney

 

ABSTRACT

 

This project proposes ways to improve the performance of airflow modeling using the Lattice-Boltzmann Model (LBM).  LBM provides an efficient means of simulating fluid flow; recent implementations run in real time on PC hardware.  However, LBM’s 3D data representation severely restricts the volume and resolution of the modeled space due to computation and memory requirements.  These constraints render LBM impractical in an open, freely-navigable 3D world.  This project’s proposed solution is to model over a selective volume using a selective modeling resolution by carrying LBM simulation inside a dynamic view frustum.

 

INTRODUCTION

 

There is a growing demand for realistic physical effects in computer graphics.  When it comes to airflow effects such as blowing wind, billowing smoke, or air turbulence, researchers seek behaviors that comply with the Navier-Stokes (NS) differential equations for incompressible fluid flow.  Derived by Claude Louis M. H. Navier and Sir George Gabriel Stokes in the 19th century, NS restates the Newtonian law of mass and momentum conservation in the context of multidimensional liquid flow (Wolf-Gladrow 2000, 7).  NS is generally impervious to conventional analytical solution techniques due to non-linearity.  Numerical methods can be used to find approximate solutions, but they are often prohibitively expensive for real-time simulation.

 

While NS deals with macroscopic fluid flow, a microscopic approach is provided by the Boltzmann equation, derived in 1872 by Ludwig Boltzmann.  The Boltzmann equation treats a dynamic fluid as a collection of microscopic particles which propagate and interact with each other.  The Lattice-Boltzmann Model (LBM) simulates this behavior on a set of discrete points regularly spaced over the simulation volume.  A simple local particle collision and propagation procedure is applied every time step in the simulation.  As time and space resolution approach infinity, LBM approaches an NS solution (Wei et al. 2003).  Due to LBM’s simplicity and data access locality, LBM has achieved real-time performance on modern PC hardware and benefited greatly from graphics hardware acceleration (Wei, Li, and Kaufman 2003).

 

Despite LBM’s promising results, it has a serious weakness inadmissible in a freely-navigable 3D world.  LBM represents the simulation volume as a 3-dimensional grid, so its performance and memory footprint depend on the volume and resolution of the modeled space.  This is problematic in a freely-navigable 3D world for two reasons.  First, the navigable volume may vastly exceed any affordable LBM grid size (unless LBM resolution is reduced below any useful threshold).  Second, LBM’s fixed resolution is dismally maladaptive to the viewer’s position in a large world.  When perspective-projected onto screen space, faraway grid points become wastefully close together, while nearby points are too far apart.  Thus, small nearby objects will experience no local airflow phenomena (unless LBM resolution is astronomically high).  At the same time, visible faraway objects will have more airflow modeling precision than noticeable by the viewer.

 

LBM’s resolution inefficiency is particularly glaring in light of the increasing popularity of level-of-detail (LOD) models, procedural geometry models, hierarchical object consolidation, and size-based visibility culling.  All of these techniques adjust geometric detail in proportion to an object’s area on the screen (e.g. they stabilize a scene’s resolution in screen space), with the goal providing adequate detail up-close, while eliminating or merging excessive detail far away.  These techniques also make fixed-resolution LBM grids very inefficient for faraway objects—the objects become very large relative to the LBM grid.

 

This project modifies LBM’s volume and resolution of simulation to achieve two goals in real time.  The first is to extend the visibly simulated airflow volume to an unlimited navigable world.  The second is to adjust LBM resolution to screen space resolution, permitting efficient use of screen space and interaction with LOD and similar objects.

 

The remaining paper is divided as follows.  Previous Work describes prior approaches to gas and airflow modeling.  The Lattice-Boltzmann Model explains the basics of the LBM simulation process.  Approaches to Adaptive LBM details several ways to adjust LBM detail to viewer position, and explains the author’s choice.  Implementation describes the demo that showcases frustum-mapped LBM simulation.  Results and Discussion address the demo’s performance, limitations, and the possibility of acceleration on graphics hardware.  Conclusion, Future Directions, References, and Demo Screenshots conclude the paper.

 

PREVIOUS WORK

 

Several approaches have been explored for simulating fluid dynamics on computer hardware.  Procedural modeling was introduced by (Perlin 1985, 287-296) and uses parametric functions to describe fluid behaviors.  This method is fast, but requires an unsystematic and difficult search for the right parameters to produce realistic results and has difficulties with environmental fluid interactions (Wei and Kaufman 2003, 6).  Physically-based modeling has been proposed by (Wejchert and Haumann 1991, 19-22), and provides an analytical solution.  Unfortunately, the computation time and memory requirements for 3D simulation are substantial (Wei and Kaufman 2003, 6).  A method of finite differences in 3D was introduced by (Foster and Metaxas 1997, 181-188); however, finite differences are inherently unstable at large time steps and restrict the simulation speed.

 

More successful approaches ensued when (Stam 1999, 121-128) provided an unconditionally stable method using semi-Lagrangian advection and an implicit Navier-Stokes solver.  This method is capable of simulating turbulent flows and can be executed in real time on a low-resolution grid.  The method suffers from turbulence decay caused by numerical dissipation, but (Fedkiw, Stam, and Jensen 2001, 129-136) proposed using vortex confinement to avert such premature dissolution by feeding energy back into vortices.

 

The above methods are “top-down” approaches to approximating solutions to Navier-Stokes (NS) equations: they transform NS into discrete elements such as finite differences, finite volumes, finite elements, or spectral methods (Wolf-Gladrow 2000, 11).  By contrast, Lattice-Gas Cellular Automata (LGCA) and the Lattice-Boltzmann Model (LBM) are “bottom-up” approaches; they simulate microscopic particle interactions modeled by the Boltzmann equation.  Given sufficient numbers of particles and time-space resolution, they approach NS globally.  The simplicity of modeling local interactions allows fast parallel implementations (such as on graphics hardware).

 

Cellular automata were introduced in 1950 and can be described as a collection of identical “cells” regularly distributed in space; each cell has an associated state, which changes during each time step depending on the states of its neighbors.  The application to fluid dynamics was initially proposed by the HPP LGCA model (Hardy, de Pazzis, and Pomeau 1973).  The HPP model used a “square tile” distribution, where binary on/off cells simulated the presence of gas particles moving in orthogonal directions.  HPP failed to simulate Navier-Stokes because the square tiles’ inadequate 4-way symmetry produced results that were non-isotropic (inconsistent for different coordinate axis orientations).  Subsequently, (Frisch, Hasslacher, and Pomeau 1986) produced a hexagonal FHP lattice and showed that 6-way symmetry was sufficient to yield the Navier-Stokes equation in the macroscopic limit.  Used together with programming techniques such as multi-spin coding, HPP and FHP can be efficiently programmed for parallel computation on desktop PCs (Wolf-Gladrow 2000, 53).

 

The problem with LGCA is its binary nature: it attempts to simulate individual particles and consequently produces grainy “black and white” distributions.  They can be smoothed by averaging over larger areas of the LGCA grid, but this makes for inefficient use of high grid resolution—performance is wasted.

 

LBM addresses the graininess problem (amongst others) by replacing the notion of individual on/off particles with continuously variable particle distributions.  Thus LBM smoothes the range of possible gas pressure/velocity vectors at each cell in the grid.  LBM has been shown to work in 2D as well as in 3D using square and cubic tiles, respectively, and a combination of orthogonal and diagonal interlinks.  The simulation process is more complex than LGCA because collisions and boundary conditions are complicated by the non-discrete particle distribution values.

 

THE LATTICE-BOLTZMANN MODEL

 

The Lattice-Boltzmann Model (LBM) simulates the microscopic movement of fluid particles, which macroscopically obey the incompressible Navier-Stokes (NS) equations governing fluid motion.  LBM subdivides space into a grid composed of regularly-spaced cells; the set of vectors connecting a cell to its immediate neighbors comprises a set of 4 discrete lattices shown in Figure 1 (Wei et al. 2003).  These vectors represent fluid particle flow along those particular directions.  Sub-lattice (a) is a zero vector representing stationary particles.

 

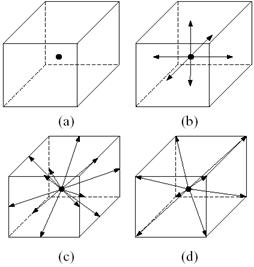
Figure 1: The four sub-lattices defined on a 3D gri;d taken from (Wei et al. 2003).

 

LBM simulation proceeds in a series of discrete time steps; each step consists of particle collision and propagation stages.  The particle collision operation is computed locally for each cubic tile.  A local collision is represented by displacing the velocities of colliding (opposite-facing) streams of fluid particles.  The restriction is that after the collision step, the total mass and momentum must be preserved.  This is accomplished by calculating an equilibrium velocity distribution based on the initial mass and momentum of fluid particles.  The post-collision velocities are calculated as the pre-collision velocities plus a scaled difference with the equilibrium distribution.  The propagation step simply moves the particle distributions one unit along their velocity vectors (e.g. to the neighboring cells).

 

The boundary conditions and object interactions are another source of concern.  The simplest approach is to use periodic boundary conditions, e.g. to assume the LBM volume wraps around on itself.  Objects can be assumed too light to affect airflow.  In this ideal scenario, no special accommodations are needed.  However, obstacles at the edges and heavy objects require special boundary treatment by using special semi-solid boundary tiles (Wei et al. 2003).

 

APPROACHES TO ADAPTIVE LBM

 

The goal of this project is to adapt LBM to permit unlimited modeling space and consistent screen space resolution.  Many different approaches are possible, some of which are discussed here.  For clarity, these approaches are categorized as preserving or distorting the LBM lattice shape.  The distortion of lattice shape may cause undesired anisotropy, instability, or other deviations compared with a better-understood regularly-spaced cubic grid.  However, distortion permits potentially higher LBM resolution efficiency, and its associated problems may be partially curable.

 

Amongst the distortion-free approaches to adaptive LBM modeling, Figure 2 shows the traditional fixed-resolution approach.  The triangle represents the view frustum (2D projection from above; 90% horizontal field of view).

 

                    

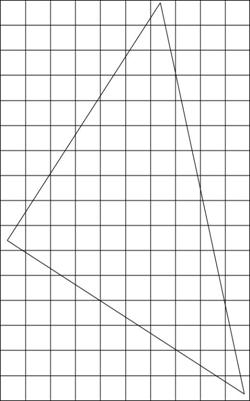
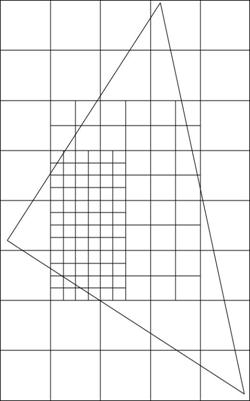
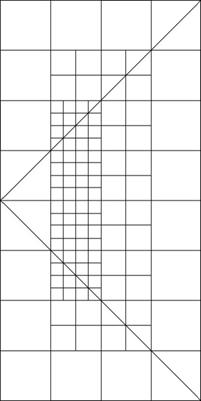
Figure 2: Conventional LBM                       Figure 3: Octtree World Space LBM       Figure 4: Octtree Screen Space LBM

 

Conventional LBM resolution grid, world coordinates advantages:

Disadvantages:

 

Figure 3 shows the concept of using octtrees to subdivide the world into a set of fixed-resolution subgrids.  Advantages:

Disadvantages:

 

Figure 4 shows the possibility of transforming the octtree approach into the camera’s screen coordinates.  Advantages:

Disadvantages:

 

                     

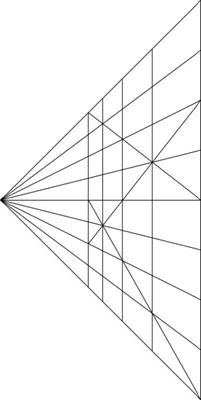
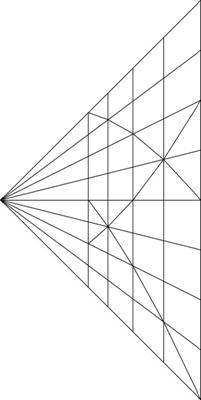
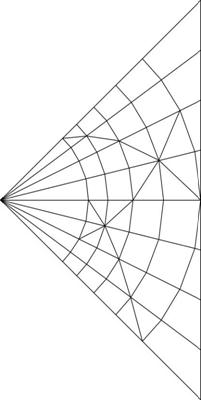
Figure 5: Projection transformation LBM    Figure 6: Geometric series LBM      Figure 7: Spheric geo-series LBM

 

Figures 5-7 show how the LBM grid can be distorted to fit the view frustum almost exactly.  In practice, it may be better to make the LBM grid a subset of the view frustum, ignoring extreme far distances.

 

Figure 5 uses a projection transformation, which has the following advantages:

Disadvantages:

 

Figure 6 uses a geometric series to make all depth slices geometrically similar to each other, to minimize distortion.  Advantages:

Disadvantages:

 

Finally, Figure 7 is a modification that holds each vertex in a slice be equidistant from the viewer.  Advantages:

Disadvantages:

 

Due to its relatively small distortion combined with highly efficient space coverage, the geometric series approach was chosen for this project.

 

IMPLEMENTATION

 

The created demo emulates a level-of-detail world where objects’ geometric detail varies with the distance from the camera.  Leaves blow across the scene, blown by the vectors in the LBM grid, with gravity effects and forces proportional to the perpendicularly exposed leaf area.  A semi-realistic world environment was created from procedurally-generated bushes, trees, and hills which are made of sphere, cylinder, and plane primitives.  The view frustum contains the LBM simulation grid, which covers 100 % of the width, 66.7% of the height, and 12.5% of the depth of the view frustum.  Because the LBM grid’s depth-wise velocity vectors are collinear and converge at the camera’s origin, the grid projects onto screen space with constant spacing.

 

When using computer software, the LBM grid can be represented efficiently as a 1D array where X and Y dimensions are scaled up to nearest powers of 2.  This way, the rightmost log2(X’) bits are reserved for the X address, the next log2(Y’) bits for the Y address, and the rest for Z; this makes addressing faster in many cases.

 

The process of mapping from world coordinates to LBM grid coordinates is fairly simple.  World coordinates are linearly transformed into view coordinates (multiplication by a matrix).  Then X and Y coordinates are divided by the Z (depth) coordinate.  Finally, the logarithm of the Z coordinate is taken by using a fast floating-point logarithm function such as: extract the exponent part by bitshifting, then add a value from a lookup table indexed on the first 8-12 bits of the mantissa.  When the Z logarithm is properly scaled, the return value would correspond to the LBM grid Z value.  Trilinear filtering may have to be used to get the closest velocity vector to the desired world position.

 

Inverse mapping from LBM grid coordinates to world coordinates is even quicker.  Use a lookup table to get the Z power of the geometric series factor; multiply grid X and Y by Z; reverse-transform from view to world coordinates.

 

The most serious performance-related problem of view frustum-mapped LBM is adapting to a changing camera position or orientation.  A 3D transformation is needed to convert vectors into the corresponding newly positioned tiles.  Additional tile information may have to be discarded.  It is the presumption here that the addressing tricks permit to make such a transformation comparable in speed to advancing the simulation 1 time step.

 

Handling collisions is similar to the conventional LBM case.  Handling propagation can be done via an addressing trick by adding an offset to the coordinates of grid lookups and modulating by X, Y, or Z.  This removes the memory-intensive task of copying velocity distribution values over each time.

 

The numerical challenges of using a distorted LBM grid are based on the problem of mass and momentum conservation.  Does particle mass K in the near depth plane correspond to the same mass in the far plane?  One approach is to say Yes, and use the known asymmetry in velocity vectors to preserve momentum.  Unfortunately, using this approach directly resulted in unstable simulation, where strong periodic gusts of wind developed in the front-to-back direction.  The other approach is to say No, and to scale the momentum of faraway particles according to their distance.  This approach produced more satisfactory results when using periodic boundary conditions.

 

It is undoubted that distortion of the LBM grid may produce at least some anisotropy and might not correctly approach the Navier-Stokes equation.  The goal is merely to be sufficiently close, so that the visual appearance, performance, and freedom of movement make view frustum-mapped LBM a competitive choice for real-time navigable 3D worlds.

 

RESULTS AND DISCUSSION

 

The demo uses OpenGL and currently runs on the Windows platform using a Pentium 4 2.26GHz with ATI Radeon 9800 at a speed of 15FPS.  Screenshots are included in the Screenshots section.  Limitations of the demo implementation include a lack of flow interaction with the environment and using periodic boundary conditions.

 

One of the advantages of classic LBM is its adaptability to graphics hardware acceleration.  The GPU has been shown to accelerate the performance by a factor of ~50 in some cases (Wei, Li, and Kaufman 2003).  The view frustum-mapped LBM method should be amenable to similar enhancements.  The differences from conventional LBM lie in distorted coordinate transformations and camera-related LBM grid recalculations.  Coordinate transformations can be handled on GPU hardware by using 1D texture lookups for algorithm functions (for transforming from world to grid coordinates) and using GPU matrix multiplication.  Camera-related transforms would be more complicated and may require two steps: going from old grid to world coordinates and then to new grid coordinates.

 

CONCLUSION

 

Due to its promising performance and realistic airflow effect appearance, view frustum-mapped LBM presents a promising alternative to conventional LBM for the purpose of airflow effects in an open, freely navigable 3D world.  Furthermore, even disregarding absolute performance, frustum-mapped LBM allows for a greater range of resolution and simulation volume than conventional LBM.

 

FUTURE DIRECTIONS

 

The project can be improved as follows.  Ways can be found to accelerate the camera movement/rotation-related LBM grid readjustment.  Also, the LBM calculations can be moved to GPU hardware similarly to (Wei et al. 2003).  This would provide a more realistic basis for comparing performance.  Finally, simulation instabilities and ways to handle momentum vs. distance tradeoffs (time and space distortion) could be further explored.

 

REFERENCES

 

R. Fedkiw, J. Stam, and H. Jensen, 2001.  Visual simulation of smoke.  Proceedings of  SIGGRAPH 2001: 129–136.

 

N. Foster and D. Metaxas, 1997.  Modeling the motion of a hot, turbulent gas.  Proceedings of SIGGRAPH 1997: 181–188.

 

U. Frisch, B. Hasslacher, and Y. Pomeau, 1986.  Lattice-gas automata for the Navier-Stokes Equation.  Phys. Rev. Lett. 56(14): 1505-1508.

 

J. Hardy, Y. Pomeau, and O. de Pazzis, 1973.  Time evolution of a two-dimensional model system: Invariant states and time correlation functions.  J. Math. Phys. 14(12): 1746-1759.

 

K. Perlin, 1985.  An image synthesizer.  Proceedings of SIGGRAPH 19(3): 287–296.

 

D. H. Rothman and S. Zaleski, 1997.  Lattice-gas cellular automata: Simple models of complex hydrodynamics.  Cambridge University press.

 

J. Stam, 1999.  Stable fluids.  Proceedings of SIGGRAPH 1999: 121–128.

 

Xiaoming Wei, Ye Zhao, Zhe Fan, Wei Li, Suzanne Yoakum-Stover and Arie Kaufman.  Blowing in the wind.  ACM SIGGRAPH/EUROGRAPHICS Symposium on Computer Animation 2003: 75-85.

 

Xiaoming Wei, Wei Li, and Arie Kaufman, 2003.  Implementing lattice boltzmann computation on graphics hardware.  The Visual Computer 2003.

 

Xiaoming Wei, Wei Li, and Arie Kaufman, 2003.  Interactive flowing of highly viscous volumes in virtual environments.  IEEE Virtual Reality 2003: 281-282.

 

Xiaoming Wei, Wei Li, and Arie Kaufman, 2003.  Melting and flowing of viscous volumes.  Computer Animation and Social Agents 2003: 54-59.

 

Xiaoming Wei, Wei Li, Klaus Mueller, and Arie Kaufman, 2003.  The lattice-boltzmann method for gaseous phenomena.  IEEE Transactions on Visualization and Computer Graphics.

 

Xiaoming Wei, Wei Li, Klaus Mueller, and Arie Kaufman, 2002.  Simulating fire with texture splats.  IEEE Visualization 2002: 227-237.

 

D. Weiskopf, M. Hopf, and T. Ertl, 2001.  Hardware-accelerated visualization of time-varying 2D and 3D vector fields by texture advection via programmable per-pixel operations.  Workshop on Vision, Modeling, and Visualization VMV ’01: 439-446.

 

J. Wejchert and D. Haumann, 1991.  Animation aerodynamics.  Proceedings of SIGGRAPH 25(4): 19–22.

 

Dieter A. Wolf-Gladrow, 2000.  Lattice-gas cellular automata and lattice-boltzmann models, An Introduction.  Springer-Verlag.

SCREENSHOTS

 

 

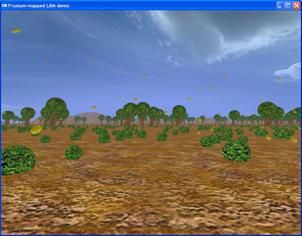
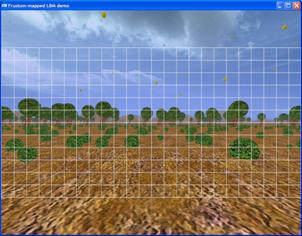
          The world with leaves blowing.                 The LBM grid projected onto screen space.

 

 

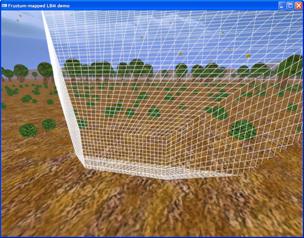
An “outsider” view of the frustum-mapped LBM grid.

 

Wireframe view of the procedural world.