|
ABSTRACT
The purpose of this project is to create 3D
engine that displays the interaction of non-rigid bodies. As a part
of our project we researched existing models for elastic and
deformable bodies and algorithms for their collision detection and
collision response. We have created a model of the object as a set
of points connected by springs of given elasticity factor k. The
model uses spring forces and damping to give elasticity to the
objects. Object collisions are determined using our collision
detection engine. After collision occurs the response is calculated
using physics laws.
MODEL OF A SINGLE
OBJECT
- Overview
The objects we are
working with are elastic and deformable bodies. They change their
shape under the influence of outside forces and then return to
their original shapes. Considering gravity as an external force,
in the real world situation, even in a state of rest, for example
sitting on a table, this type of object will have a slight
deformation of shape and due to it the springs will not be in
equilibrium. This can be used to model objects made out of rubber,
jell, metal or other similar substances.
These objects
behave according to a set of rules commonly used in physics
models. They maintain constant velocity and shape if no external
forces are applied (Newton’s First Law). Without deformation the
object has six degrees of freedom (three for translation and three
for rotation). If an external force is applied to some part of the
object it deforms to find a state of rest where its internal
energy is balanced by its external forces. If the influence of the
force stops, the object returns to its previous shape, after any
vibrations have dampened. We will assume that objects are
non-breakable, do not change their elasticity over time, and do
not deform permanently.
- Prior Work
Over the past two
decades, people in academia and industry have been working on
simulating physically realistic elastic objects. Different models
have been developed over time. Most of them use some kind of
elasticity rule combined with different constraints Terzopoulos
and Witkin presented the Hybrid model [4],
where an object has a reference component, which represent shape
and displacement components. These components represent a
deformation from the initial shape. In later research other models
and ideas were introduced, including the concept of local and
global deformations [5];
using extra layer coatings [8];
using elastic grids with additional constraints. Recently,
adaptive models for elastic and deformable bodies were developed;
some of them use mass-spring system similar to the one we used for
our project [6].
Compared to these models, our model is quite simple; however it
includes all the main factors needed to animate and provide
interaction between elastic and deformable bodies.
- Description
For our
models an object is represented as a mesh of polygons, namely
triangles. The edges of the triangles possess the physical
qualities of springs. Vertices have properties of rigid bodies
that are connected by springs. Vertices have only three degrees of
freedom – they can move in space but cannot rotate. If a distance
between two adjacent vertices shortens, the spring which connects
them forces them to move farther from each other and vice versa.
The principal idea behind our model is that each point
behaves as an independent body, or particle, and only spring
forces of its direct neighbors affect velocity and acceleration of
this point. In our model we do not maintain information about
linear and angular acceleration or the velocity of the object, and
instead we only store the accelerations and velocities of each
particle.
-
Physics Involved
As mentioned
earlier, the main forces that move and deform the objects are the
internal spring forces of is edges. The force applied on each
vertex is calculated by the spring equation [1]:
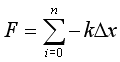
Where k is
elasticity constant of the object and Dx is the displacement of
the length of the edge, and n is number of direct neighbors of the
vertex. Although we work in 3D, this force is calculated as
projection on 1D space of each edge.
While working with
springs the problem of damping arises. In a real world, springs do
not oscillate forever because of the loss of internal energy. In
graphics and mechanics the loss can be simulated by applying a
damping on the spring. There are several ways to do damping:
viscous damping, linear damping, or Rayleigh’s damping [1].
For this project we have chosen the viscous damping. After
including damping the formula for the force applied to each vertex
changes to the following:

Where c is
a damping constant and v is the velocity of a vertex.
The
displacement of each vertex is calculated using Newton’s Laws and
basic formulas for the motion of the body [2]:
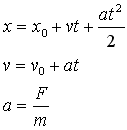
To achieve the
best performance, some assumptions should be made about the
object. As each vertex of an object is assumed to have the same
mass, the distances between adjacent vertices should be
approximately equal to each other. So even if it is not needed for
the appearance, the mesh of the object should be equally
distributed over the object’s surface, otherwise a more
sophisticated algorithm is needed to compute mass of each vertex
so that mass of the body is uniform.
-
Algorithms and Other
Issues
After deriving the formulas for the
vertex forces there are two problems that need to be solved:
creating a data structure for the object and applying linear
algebra for projection of 3D space to 2D or 1D.
The data
structure of the model includes a set of vertices with velocities
and accelerations for each vertex. Each vertex also holds a list
of its direct neighbors as well as the initial (rest) distances to
each of them. So in order to update the position of a vertex, we
calculate the force applied (using the difference between the
current and initial distances between the vertex and each
neighbor), then update acceleration and velocity, and finally
compute the displacement from previous position. There is also set
of faces (triangles) and edges stored for each object and are used
later for the collision detection and rendering.
The
principal advantage of our model is that natural behavior of the
elastic object can be achieved using a number of easily computed
algebraic physics equations of degree at most two. The object mesh
is easy to create using standard 3D graphics tool, for example 3D Studio Max
[13].
Note that our model does not necessarily preserve the volume of
the body. If this is desired, additional constrains must be added.
Also the elasticity constant depends on the complexity of the
object and has to be calculated for each different object. One of
the disadvantages of our model is that creating objects with no
elasticity (rigid bodies) results in strong oscillation which
damping cannot handle. For this reason, non-elastic objects are
handled by a different method.
MECHANICS
BEHIND OBJECT INTERACTION
- Overview
Given the object
model presented in the previous section, the next building block
to consider is how to combine them into a single world. One of the
factors involved in this is updating movements between objects,
namely applying the appropriate forces to each object and updating
their coordinates over some time step. Following any type of
non-predetermined movement, some sort of collision detection
algorithm is run between all appropriate pairs of objects. If any
contact is detected, all of the information regarding the
collision must be extracted and the appropriate collision response
mechanism is applied.
Typically in complex rendering
programs or games, the objects in space would be contained in some
type of data structure, such as an octree or kd-tree as proposed
by Samet [11].
Such an implementation can provide several performance gains,
including rendering of objects and limiting the pairs of objects
to which the collision test must be applied. In the rendering
process these data structures can help to determine whether an
object needs to be drawn on the screen. For example the
partitioning nature of these structures organizes spatial
information such as objects in such a way that they can determine
when other objects are very close to it or when one is occluded
behind another. These properties help when trying to decide what
objects need to be drawn or need to have complex operations
applied to them such namely collision detection. Inaccuracies in
the collision detection can arise when the time step between
screen updates is large enough that the physical forces would
place them on opposite sides of each other. To compensate for this
scenario the objects typically require being sufficiently scaled
in size or a smaller time step has to be used in the collision
detection process.
- Prior Work
There are many methods
that have been proposed for collision detection. Generally all
objects have some sort of boundary or more commonly a radius in
which they are contained within, and whenever another object comes
sufficiently near, a series of calculations are performed to see
if there was an actual collision. When dealing with convex
objects, this method works well because the object can be
simplified to a sphere or ellipse and your chances of finding a
collision are higher in an early time step. With concave objects
there is a chance that the object could be very complex and a
collision might not be found until several time steps later. To
get around this problem this idea has been taken to another level
with the use of hierarchal collision detection [12].
As the name suggests, there are layers of boundaries or radii that
have to be penetrated before a collision is detected. In the case
of concave objects this works well because, after the primary
radius has been penetrated, the collision detection is done
against the next set of radii and so forth, as necessary. This
works well when the nature of the object is sparse or has convex
substructures, because it increases the accuracy of the collision
detection while reducing the need for computationally expensive
algorithms.
When it is determined that the collision
boundary has been penetrated, it is required to be known exactly
if there was a collision and where. There are various algorithms
that can calculate this but the overall method used by most of
them is to compare all the faces or edges of one object and see if
any of them lie within the boundaries of the other object. While
simple in concept, most techniques require several floating-point
calculations to check against many edges and points of every
polygon in one object to the other. Typically there is a check to
see if either point of any edge in one object penetrates any
polygon in the other object. This procedure is run twice,
reversing the roles of edges and polygons between the two objects.
If this does not reveal an intersection, all the individual faces
and edges are checked to see if they are coplanar and/or
coincident. When naively implemented, this technique will still
work but can be very expensive if the object consists of a large
number of edges. In this instance some type of selection against
the object is done in order to select a minimal set of edges and
polygons to check against. For example, if the relative centers of
two objects can be determined and the two points used as a vector
and treated as the normal of a plane, then it suffices to test
only points that lie on one side of that plane. In the situation
where the objects are represented by polynomial equations, it is
common to check if the surfaces defined by these equations
intersect using any of several techniques based on integral
calculus.
After it has been determined that a collision
has occurred, we need to know where the collision has occurred and
make an appropriate response to the point of intersection. In this
stage, the need for accuracy in the location of the collision is
the driving factor for what collision information should
collected. In one case we can attempt to calculate the actual
point of collision and try to isolate all the elements involved,
such as the direction of the collision and the force being applied
at that point. At the time of collision, if it is determined that
the two objects have penetrated each other, somewhere between the
previous time step and the current step there was a point in time
when the collision first occurs. So in order to find the instance
of collision, the collision data is recalculated using a time step
that is a half of the current time step and the previous. This
process is repeated until there is collision without penetration
or until some threshold is met. While this solution provides
accuracy in the collision data, it is computationally expensive to
repeat several calculations, which can produce redundant
information between iterations. What can happen instead is that
all the information about the collision can be collected and then
approximate what the real collision information data should
be.
- Algorithms Used
In our
implementation we maintain a collection of objects, and then at
arbitrary time intervals we update their positions in space, check
for collisions and respond appropriately to them and repeat this
process as necessary [10].
For the collision detection step, we used a variation of a ray to
triangle intersection algorithm. For any two objects that we find
to be within each other’s collision boundary, we iterate over the
edges of one object and check for any intersection with any of the
planes of the triangles that make up the other object. If the edge
has been found to be crossing or touching the plane, the point of
intersection with the plane is then calculated. If that point is
contained within the triangle on that plane then we have detected
a collision. As we continue to iterate over the rest of the edges,
we mark all the edges and points of one object that were found to
have intersected the other object. Then with this set of edges, we
run a depth-first search against the graph of the object’s
polygonal mesh to collect all the points that are contained within
the other object. Once this set is complete, we apply our
collision response system with the appropriate physics, as
described in the previous section.
IMPLEMENTATION
DETAILS
In order to
illustrate the models and algorithms we created and used, we
developed an application that takes text file of meshes and their
initial velocities as input and animates the behavior of these
objects. This application was developed using C++ under the
Microsoft Visual C++ .NET Compiler and the Standard C, OpenGL, STL
libraries and the Win32 API. The program structure is intended to be
cross platform compatible so there are areas where things such as
the timing mechanism is abstracted away into its own
object.
You can download the source code here and
text files with model meshes here.
The
most general class in our program is World, which contains list of
objects displayed on the screen (EObject). Each object has list of
faces (Triangle), edges (Edge), and points (GLPoint). The principal
functional elements of the program, including collision detection,
collision response, and each point location update can be found in
the source file EObject.cpp. In the main loop for our program, after
all models have been loaded into memory and initialized, we iterate
over our collection of objects calling an update on their movements
using the time span between the last iteration and the current as
the time step. After the updates, we check all appropriate objects
for collisions against each other. If a collision is found, we apply
the appropriate collision response mechanism for that
collision.
In Windows, the standard timing library did not
allow for precision in timing beyond seconds so we had to use the
WIN32 API to achieve greater precision. Our program uses a single
thread for execution. Rather than using the timestamps from the
system clock which would include time allocated to other programs by
the processor, we used the timestamp for the lifetime of the
thread.
CONCLUSIONS AND
SCREENSHOTS
In the project
we presented a 3D engine for the animation of non-rigid bodies. We
were able to achieve natural behavior of elastic bodies and their
collisions. Here is set of screen shots which were taken from the
engine:
Animation of multiple objects falling on the ground and
interaction with each other.
A box falling on the ground and flipping
over.
POSSIBLE FUTURE
WORK
There
are several ways to extend this project. The first is to improve
current engine. This might include adding global constraints such as
preserving object volume; optimizing the collision detection
algorithm by creating more sophisticated bounding boxes for each
object, improving the algorithm for spring damping. The other
possible direction is to use a similar system to create other types
of flexible objects, for example cloth [9] or
hair. As longer term work, it might be possible to extend our
approach to create a model for much more general classes of
substances. That would require adding more physically realistic
elements into the model, creating uniform mesh over all the volume
of the object, and finding specific constraints to satisfy
properties of different types of the material
REFERENCES
- Tongue, Benson H., “Principles of Vibration,”
1996
- Hibbeler, R. C., “Engineering mechanics.
Dynamics,” 8th ed, 1997
- Bourge, David M. “Physics for Game Developers”,
November 2001
- Terzopoulos,
D., Witkin, A, “Physically based models with rigid and deformable
components,”
Computer Graphics and Applications, IEEE, Volume:
8 Issue: 6, Nov 1988, Page(s): 41 -51
- Metaxas,
D., Terzopoulos, D., ”Dynamic 3D models with local and global
deformations: deformable superquadrics,”
Pattern Analysis and
Machine Intelligence, IEEE Transactions, Volume: 13 Issue: 7, Jul
1991, Page(s): 703 -714
- Barr,
A., Cani, M.-P., Debunne, G., Desbrun, M.,”Adaptive simulation of
soft bodies in real-time,”
Computer Animation 2000.
Proceedings, 2000, Page(s): 15 -20
- Wang,
J.-F., Wang, Y.F., “Surface reconstruction using deformable models
with interior and boundary constraints,”
Computer Vision,
1990. Proceedings, Third International Conference, 4-7 Dec 1990,
Page(s): 300 -303
- Cani-Gascuel,
M., Desbrun, M., “Animation of deformable models using implicit
surfaces,”
Visualization and Computer Graphics, IEEE
Transactions, Volume: 3 Issue: 1, Jan-Mar 1997, Page(s): 39
-50
- Eberhardt,
B., Strasser, W., Weber, A., “A fast, flexible, particle-system
model for cloth draping,”
Computer Graphics and Applications,
IEEE, Volume: 16 Issue: 5, Sep 1996, Page(s): 52 -59
- Miller,
Kurt “flipCode - Tutorial - Collision Detection” Jan 2000. Jul 14,
2002
- Samet, Hanan, “Design and Analysis of Spatial
Data Structures,” Addison-Wesley, Reading MA.
- Ramaekers,
Marc, “Hierarchical Collision Detection Methods” May 1999. Jul 12,
2002
- “Discreet products - 3ds max” http://www.discreet.com/products/3dsmax/

|